Warning You're reading an old version (v5.0) of this documentation.
If you want up-to-date information, please have a look at master.
Nonlinear EM Inversion
This section is an overview of MARE2DEM’s non-linear inversion approach as that may be helpful for understanding the various parameters in the input files and for learning how the inversion part of the code works. It is also provided as background for readers that are new to EM modeling and inversion, although by no means is this review broad enough to substitute for a proper EM inversion tutorial paper or book chapter.
MARE2DEM uses a form of regularized Gauss-Newton minimization that is known in the geophysical community as Occam’s inversion. Detailed descriptions of the Occam method can be found in the References and references therein.
The goal of EM inversion is to find a sensible model that fits the observed data. One of the main issues with geophysical inversion is that there are only a finite number of data and the data have noise (aka uncertainty), and thus there are either no models that can fit the data or there are an infinite number of models that can fit the data. EM inversion is also ill-posed, in that small amounts of noise can greatly impact the space of models that are compatible with the data. Thus the goal of EM inversion is to slice through the infinite number of data-fitting models and pull out only the main model features that are absolutely necessary to fit the data. To do that, we need both a measure of data fit as well as a metric of the variations in model structure and then we can optimize the solution about those metrics.
Occam’s inversion seeks to minimize the following unconstrained regularized functional:
The first term is a norm of the model roughness and this is used to stabilize the inversion process, since EM inversion is almost always ill-posed with a nonunique solution. The model roughness is computed by applying a roughness operator \(\mathbf{R}\) to the elements of the model parameter vector \(\mathbf{m}\). For EM inversion, the model vector \(\mathbf{m}\) contains the \(\log_{10}\) resistivity for each free parameter cell. The roughness operator \(\mathbf{R}\) approximates the spatial gradient in the model free parameters (see Model Roughness for more details). Thus the roughness operator is a measure of variations in the model; the minimization of this this quantity during the data inversion helps steer the inversion towards simple models with the minimum amount of structure required to fit the data. This type of inversion often referred to as a smooth inversion. The parameterization with respect to \(\log_{10} \rho\) ensures that resistivity remains positive during the inversion. If jumps in resistivity are desired at certain free parameter boundaries, the corresponding elements of \(\mathbf{R}\) can be relaxed (partially or fully set to 0).
The second term is not typically used, but we include it here for completeness. It is a measure of the difference of \(\mathbf{m}\) from an a priori preference (or prejudice) model \(\mathbf{m_*}\). The diagonal matrix \(\mathbf{P}\) contains non-negative scaling parameters that determine the relative weighting between the preference penalty norm and the model roughness norm. Preference model values, if used at all, are typically desired for a only few model layers and the corresponding diagonal elements of \(\mathbf{P}\) will be positive values, whereas all other values will be zero. Like the model roughness norm, the preference norm is a regularizer that acts to stabilize the inversion and keep it from producing wildly oscillating resistivity structure.
Finally, the third term is a measure of the misfit of the model’s forward responses \(F(\mathbf{m})\) (i.e., the CSEM or MT responses for model \(\mathbf{m}\)) to the data vector \(\mathbf{d}\). There is no restriction on the data vector \(\mathbf{d}\). For example, it can contain data from multiple transmitters, receivers and frequencies, and can include MT, CSEM, airborne and borehole data. The forward operator \(F(\mathbf{m})\) acts on the model vector to create the corresponding EM or MT responses (or both) and is non-linear (compare this to gravity or magnetics where the operator is linear and and be written as the matrix-vector product \(\mathbf{G m}\)). The forward operator \(F(\mathbf{m})\) contains all the physics of the problem, the numerical method used to approximate the physics, as well the data geometry, frequencies, and other fixed data and model parameters.
\(\mathbf{W}\) is a data covariance weighting function and is here selected to be a diagonal matrix with elements corresponding to inverse data standard errors. \(\mathbf{W}\) weights the relative contribution of each datum to the misfit based on its uncertainty. Thus, data with large errors are scaled to limit their influence, while data with small errors will have a bigger impact on the misfit budget.
\(\chi_{*}^{2}\) is the target misfit and its inclusion illustrates that minimizing \(U\) does not necessarily find the best fitting model, but rather a smooth model that is within the specified target misfit. The target misfit \(\chi_{*}^{2}\) is usually chosen so that the root mean square (RMS) misfit \(x_{rms}\) is equal to unity:
where n is the number of data and \(s_{i}\) is matrix element \(W_{ii}^{-1}\), the standard error of the ith datum.
The Lagrange multiplier \(\mu\) serves to balance the trade-off between the data fit and the model roughness and model preference. One of the main innovations of the Occam method is the automatic adaptive selection of \(\mu\).
Minimizing \(U\)
Minimizing equation (2) is done in the usual way, by taking its derivative with respect to the model parameters and setting that equal to zero. Hence, this type of minimization is often referred to as a gradient-based inversion, since the gradient is used to move in the direction that minimizes the functional; this contrasts with stochastic inversion methods that use some form of guided random walk to find the minimum (e.g. Bayesian inversions using the MCMC method). Gradient inversion methods will converge to the minimum much more quickly than stochastic methods, but taking the derivative can be computationally more expensive. Further gradient inversion methods often just find the minimum, whereas stochastic methods can be used to map out the space of model parameters fitting the data about the minimum best fitting model, and thus offer estimates of uncertainty in the inverted model parameters. However, while stochastic methods have a lot to offer, at the moment they are much too slow for most practical 2D inversions as they require 100,000’s to millions of forward solutions, whereas the gradient inversion using in MARE2DEM typically requires less than about 100 forward solutions.
Taking the derivative is a tad more complicated than what you might be used to from undergraduate calculus, since now the derivative is with respect to a vector of model parameters and the forward operator is non-linear. So let’s walk through the derivation details. The norms in equation (2) can be expanded to be
where the residual vector \(\mathbf{r} = \mathbf{d} - F(\mathbf{m})\). We mentioned that this is a non-linear problem and so one of the first things we do is to linearize the problem about a model \(\mathbf{m}_2 = \mathbf{m}_1+\Delta\), with forward response
where \(\boldsymbol{\epsilon}\) is the error in the linear approximation and \(\mathbf{J}\) is the Jacobian matrix of partial derivatives of the forward response with respect to the model parameters:
which has the elements:
where i denotes the ith datum and j denotes the jth model parameter. Thus the Jacobian is a linear approximation of the model space gradient about \(\mathbf{m}_1\). If the model step size is small, this may be accurate but if the step size is too large it will be inaccurate (imagine taking the slope of a point somewhere on a cubic function and notice how if you move a small distance left or right the slope is accurate at predicting the function value, but if you move to far it will be way off from the actual function value).
Rewriting the functional for \(\mathbf{m}_2\) and inserting the linearized expression for \(F(\mathbf{m}_2)\) gives
where \(\hat{\mathbf{d}} = {\mathbf{d}} - F(\mathbf{m}_1)+ \mathbf{J}_1\mathbf{m}_1\) and the linearization error \(\xi=\boldsymbol{\epsilon}^T \mathbf{W} ^T \mathbf{W} \boldsymbol{\epsilon}\). We will assume the model step size \(\Delta\) is small enough that \(\xi\) can be neglected in the remaining steps. We can find the stationary point by taking the derivative with respect to \(\mathbf{m}_2\), giving
Setting this equal to zero to find the stationary point and rearranging terms yields
In equation (3), you can see that the model roughness and preference act as dampening terms in the matrix; they help the matrix avoid being singular when the Jacobian terms are numerically very small. Further, the tradeoff parameter \(\mu\) acts to scale the dampening created by these terms. The linear system in the equation above can be solved to yield \(\mathbf{m}_2\), given the forward response and Jacobian matrix terms computed about the starting model \(\mathbf{m}_1\). This leads to an iterative approach for finding the best fitting model. Given a starting model, a new model is found by solving the linear system above. The Jacobian and forward response of that new model are then used as the input model to solve the equation above for another new model. This proceeds iteratively until a good fitting model has been found.
Note that instead of solving for \(\mathbf{m}_2\), the problem can also be recast to solve for \(\Delta\). While the resulting model update equation for \(\Delta\) is similar to but slightly different than eq. (3), the resulting model \(\mathbf{m}_2\) will be the same either way.
Parallel Dense Matrix Computations
For large model and data vectors, the matrix operations in eq. (3) that involve the Jacobian are expensive since it is a dense matrix wiht many numbers to be multiplied and summed. These operations can require a significant computational effort as the dense matrix multiplications for a \(n \times n\) size matrix requires of order \(n^3\) operations, with similar requirements for solving the dense linear system. MARE2DEM uses the ScaLAPACK library to efficiently carry out the matrix multiplications and solve the linear system in parallel using all processing cores. The figure below shows how long these operations can take and how they can be sped up by using more processing cores. Notice how a relatively large 2D problem with 80,000 model parameters and data requires over an hour when run on only 8 cores (i.e. a single cluster CPU node), but can be sped up to less than two minutes when run on 480 processing cores.
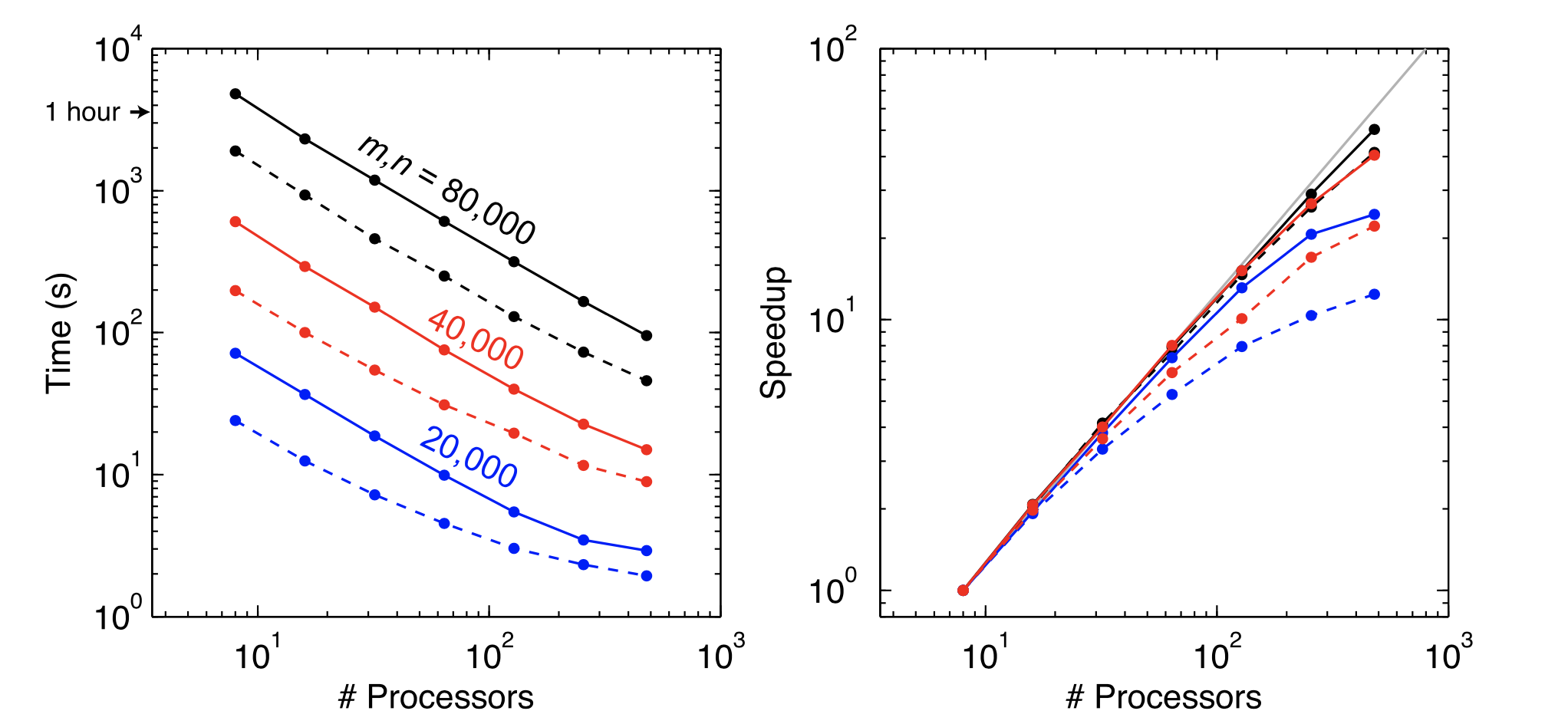
Fig. 41 Runtime scaling (left) and relative speedup (right) of the ScaLAPACK routines used for the dense matrix operations in MARE2DEM for a \(m \times n\) size matrix . Solid lines show the time to compute the dense matrix product \((\mathbf{W} \mathbf{J} ) ^T\mathbf{W} \mathbf{J}\) using the routine PDSYRK. Dashed lines show the time required to solve the linear system in eq. (3) using the Cholesky factorization routines PDPOTRF and PDPOTRS. Relative speedup is here defined to be \(t_8/t_p\), where \(t_8\) is the time taken on eight processing cores and \(t_p\) is the time required on \(p\) processors.
Finding the Optimal \(\mu\)
A key step in the inversion process using eq. (3) is the careful selection of the tradeoff parameter \(\mu\). The Occam method dynamically selects \(\mu\) during each inversion iteration by carrying out a line search for the value of \(\mu\) that produces a model (via eq. (3)) with the lowest RMS misfit. If instead the lowest misfit is larger than the input model’s misfit, the model step size is cut in half and the line search is carried out again. This repeats until a better fitting model is found (or the inversion gives up if no better fitting model can be found). It can take some time to find the minimum RMS, and in the early iterations of the inversion, often the RMS that is found is still really large. Thus in [Key16] we came up with a fast Occam method where the linear search is terminated early if the process finds a model with a significant decrease in misfit from the initial input model misfit. This can result in far fewer forward calls. The figure below shows and example of how the regular and fast Occam methods converge. Both found the same model structure, but the fast Occam method required far fewer forward calls.
For the fast Occam method, the cutoff decrease in misfit is defined in
the Resistivity File (.resistivity) using the misfit decrease threshold parameter,
which has a default value of 0.85. This means the line search terminates
early if it finds a model with an RMS misfit that is a factor 0.85 or less than
the input model’s RMS misfit.
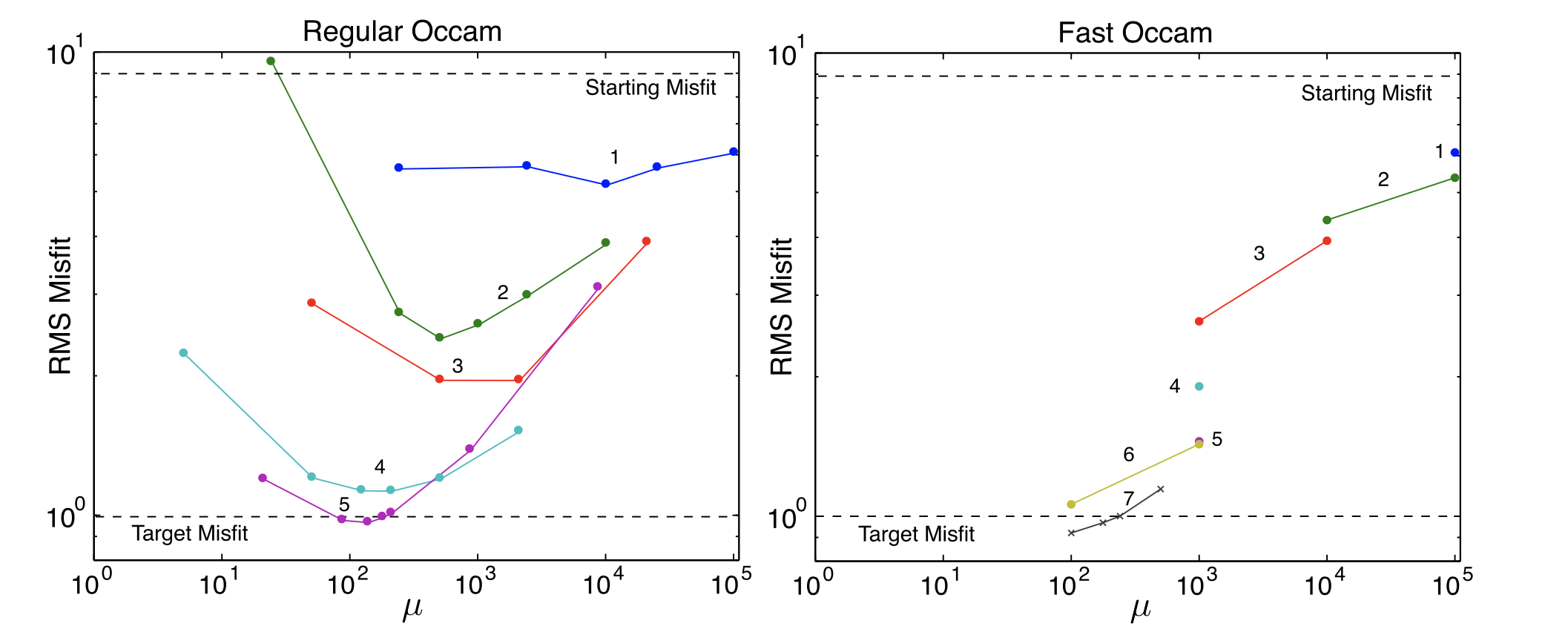
Fig. 42 Convergence of the regular Occam and fast Occam algorithms. Colored dots show the misfit for each forward call during the line search minimization of each Occam iteration. Numbers next to the coloured symbols and lines denote the iteration number. The fast Occam approach found an acceptable model at RMS 1.0 using far fewer forward calls.